Lingo教程

前言

这里是课程笔记。
这门课是偏实践的。
事实上，Lingo非常简单。

基本界面与解方程

Lingo基本界面

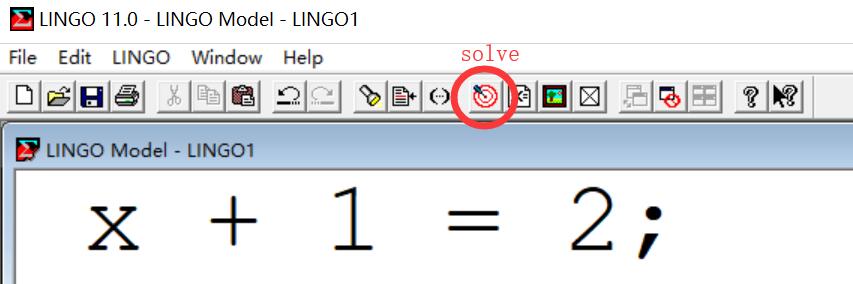
（点击Solve，结果将在Solution Report中给出）

用Lingo解方程

（每个方程都应当以;结尾）

Lingo变量

• Lingo默认所有变量为大于等于0的数字
• 使用@free函数使变量定义域为R
• Lingo变量名不区分大小写
• Lingo变量名由字母、数字、下划线组成，且以字母开头

线性规划基础

• 一个线性规划中只含一个目标函数
• 求目标函数的最大值或最小值分别用max=...或min=...来表示
• 注释语句以!开头，以;结尾
• 非线性规划基本得不到全局最优解

集合与矩阵

生产一维矩阵

sets:
factory /1..6/ : a,b;
plant /1..3/ : x,y;
endsets

• a、b为1×6矩阵，x、y为1×3矩阵
• factory和plant都是制造矩阵的“工厂”，但它们是两家不同的工厂
• factory工厂后面的/1..6/说明它专门生产1×6的矩阵
• factory、a、b都是任意取的变量名
• a、b由factory产生后，与factory再无关联
• Lingo通过sets:和endsets表示创建矩阵的起止

矩阵的赋值

• Lingo通过data:和enddata表示矩阵赋值的起止，即赋值语句写在两者之间
• 待求解的矩阵不用赋值
• 需要赋值的矩阵必须对每个元素都赋值

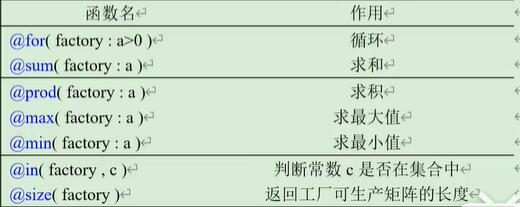
循环与求和

@for( gc(i) : a(i)*x(i)=S )，其中gc生产1×5的矩阵，表示循环次数，即a(1)*x(1)=S, ..., a(5)*x(5)=S
@sum( gc(i) : x(i) ) = 5000，其中gc生产1×5的矩阵，表示循环次数，即x(1) + ... + x(5) = 5000
（整个程序以model:开头，以end结尾）

工厂合并

sets:
factory /1..6/ : a,b;
plant /1..3/ : x,y;
Cooperation(factory, plant) : c;
endsets

• c为6×3矩阵
• Cooperation是任意取的变量名

运算符与内置函数

运算符

关系运算符

Lingo只有三种关系运算符：=、>=、<=（>和<视作>=和<=）
若想严格表达A大于B，可以用以下方式

B = 10;
e = 0.0001;
A - e > B;

逻辑运算符

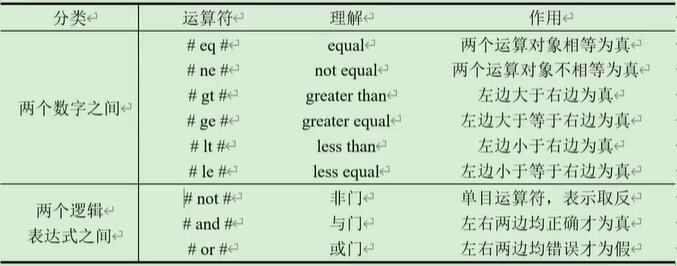
逻辑运算符仅出现于for循环、sum求和、if判断

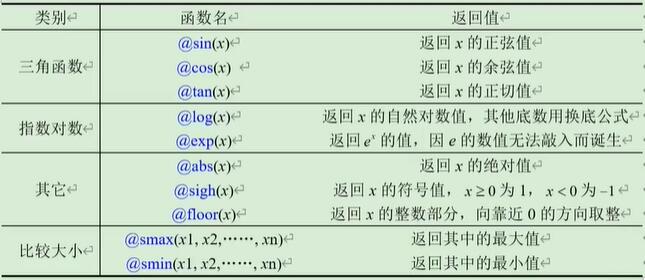
内置函数